IT/모바일
합성곱 신경망의 발달 배경
이론상으로 인공 신경망은 실수 공간에서 연속하는 모든 함수를 근사할 수 있다고 합니다(이를 보편 근사 정리universal approximation theorem라고 합니다). 하지만 무한히 많은 뉴런을 사용하는 네트워크는 만들 수도 없고 만들더라도 학습 과정에서 여러 문제가 있을 것입니다. 4장에서 배웠던 인공 신경망 모델을 사용하여 이미지 데이터에 적용해보면 사실 성능이 그렇게 잘 나오지 않는데 그 이유는 실제 예를 들어보면 쉽게 이해할 수 있습니다.

컴퓨터의 시각에서 본 그림(https://brohrer.github.io/how_convolutional_neural_networks_work.html)
앞의 두 그림은 사람이 보기에 그냥 X와 기울어진 X입니다. 하지만 컴퓨터의 입 장에서는 전혀 다른 값으로 인식됩니다. 위와 같은 이미지를 입력으로 받아서 X 인지 O인지 구분하는 모델을 만든다고 생각하면 입력 층의 뉴런의 수는 9×9로 81개가 되고 최종 결괏값은 2개(X 또는 O 클래스)가 됩니다. 그런데 왼쪽 그림처럼 기울어지지 않은 X로 학습한 모델이 오른쪽 이미지를 입력으로 받으면 기존의 학습 데이터와 다르기 때문에 제대로 예측하지 못할 것입니다. 기울어진 모양 이외에도, 한쪽 선이 짧은 X도 있을 수도 있고 전체적으로 특정 방향으로 쏠린 X도 있을 수 있습니다. 이런 예외적 모양이 들어올 때마다 인공 신경망 입장에서는 결과적으로는 같은 의미를 가지는 조금씩 다른 입력에 대해 가중치들을 학습시켜야 하고, 이미지의 크기가 커질수록 이런 변형의 가능성은 더 커집니다.
하지만 포유류나 인간의 시각 체계는 이러한 변화에 강하다는 특징이 있습니다. 이에 착안하여 동물의 시각 뉴런에 대한 연구가 이루어졌고, 1980년대 네오코 그니트론Neocognitron을 거쳐 얀 르쿤Yann LeCun 교수에 의해 합성곱 신경망convolutional neural network(CNN)이 탄생했습니다. 합성곱 신경망에는, 국소적인 영역을 보고 단순한 패턴에 자극을 받는 단순 세포와 넓은 영역을 보고 복잡한 패턴에 자극을 받는 복잡 세포가 레이어(계층)layer를 이루고 있다는 관찰이 녹아들어 있습니다.
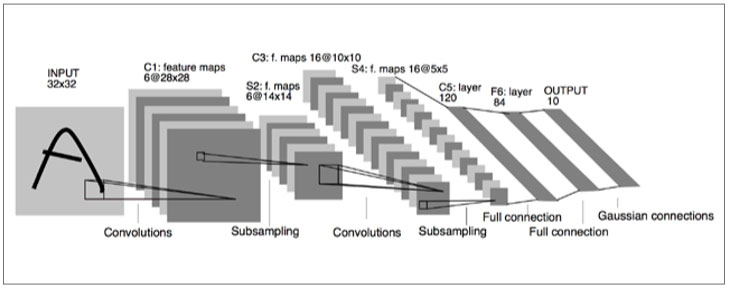
LeNet-5의 구조(http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf)
1998년에 발표된 LeNet-5의 구조를 살펴보면 이미지가 들어왔을 때 특정 영역에 대하여 합성곱 연산과 서브샘플링을 적용하는 것을 반복하고, 나중에는 완전연결full connection 및 가우시안 연결Gaussian connection을 사용하여 최종적인 결괏값을 내는 방식입니다.
합성곱 연산 과정
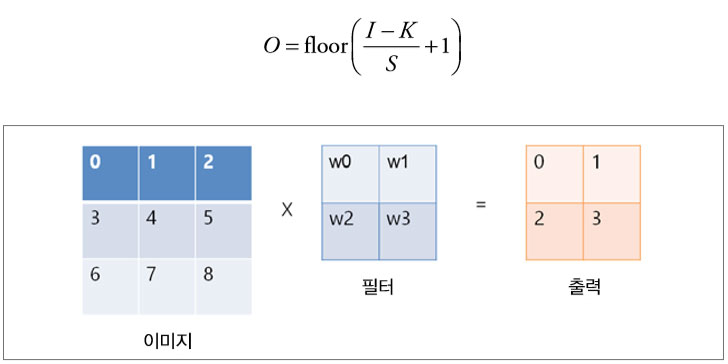
우선 합성곱 연산이 무엇인지부터 알아보겠습니다. 처음 보는 분도 있겠지만 사실 합성곱 연산은 오래전부터 있었던 수학 개념입니다. 합성곱 신경망에서는 하나의 함수가 다른 함수와 얼마나 일치하는가의 의미로 사용됩니다. 우리가 책을 읽을 때 왼쪽 위부터 오른쪽으로 그리고 다음 줄로 넘어가서 읽는 과정을 반복 하듯이 합성곱 연산은 하나의 필터filter(커널kernel이라고도 부릅니다)에 대해, 이미지를 쭉 지나가면서 이미지의 부분 부분이 필터와 얼마나 일치하는지 계산합니다. 다음 그림을 예로 계산 과정을 살펴보겠습니다.
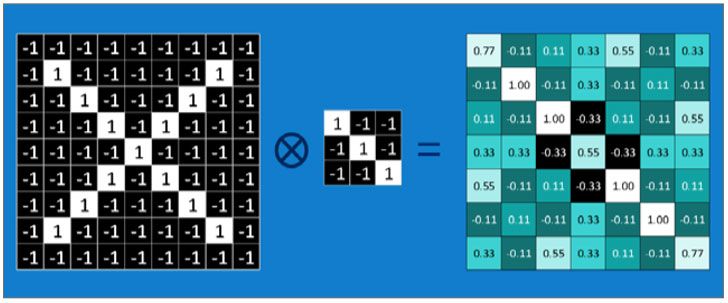
합성곱 연산의 예시
그림의 결과에서 왼쪽 맨 위의 0.77이 나온 과정을 설명하겠습니다. 입력 이미지에서의 빨간 박스 부분과 필터 간의 요소들을 각각 1대 1 대응으로 곱해서 총 합을 구하고 9로 나눠서 평균을 구했습니다. 그 후에는 입력 이미지에서 빨간 박스 부분을 한 칸 오른쪽으로 이동한 후 연산을 하면 -0.11이라는 수가 나오는데 이 수치는 입력 이미지의 해당 부분이 필터와 얼마나 일치하는지를 의미한다고 보면 됩니다. 결과 부분에서 1.00에 해당하는 부분들이 바로 필터와 이미지가 완벽히 일치하는 부분들입니다.
방금 든 예시에서는 필터의 크기가 3×3이었지만 필터의 크기는 자유자재로 지정할 수 있으며 한 칸씩 이동하던 단위 역시 자유자재로 바꿀 수 있습니다. 이동하는 단위는 스트라이드stride라고 부릅니다. 하나의 이미지에 대하여 여러 개의 필터를 적용할 수 있으며, 필터 하나당 입력 이미지 전체에 대한 필터의 일치 정도가 나오는데 이를 활성화 지도activation map 또는 특성 지도feature map라고 부릅니다. 하나의 이미지에 필터를 3개 사용한다면 활성화 지도 역시 3개가 생성되는 식입니다. 활성화 지도의 크기는 입력 이미지와 필터의 크기, 스트라이드 크기에 따라 결정되는데 입력 이미지의 크기를 I, 필터의 크기를 K, 스트라이드를 S라고 하면 활성화 지도 O의 크기는 다음 식과 같습니다(floor는 바닥 함수를 뜻합니다. 내림 함수, 버림 함수라고도 합니다).
간단한 합성곱 연산
합성곱 신경망 역시 신경망이기 때문에 4장에서 배운 인공 신경망의 형태로도 연산을 표현할 수 있습니다. 간단하게 3×3의 입력 이미지에 2×2 필터, 스트라 이드 1을 적용해보면 57쪽 그림의 연산이 다음과 같이 변환되는 것을 알 수 있습니다.
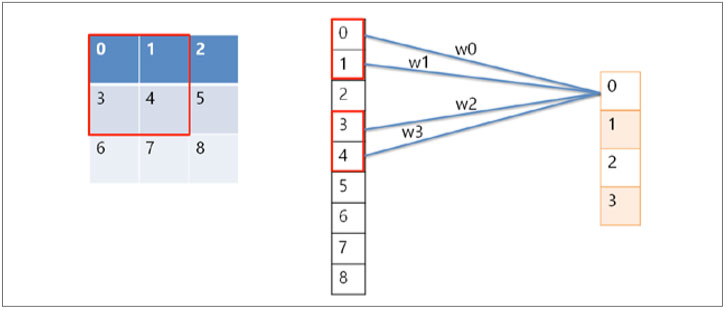
신경망 형태로 표현한 합성곱 연산
즉, 합성곱 연산도 인공 신경망의 일종이라고 볼 수 있습니다. 대신 하나의 결괏값이 생성될 때 입력값 전체가 들어가지 않고 필터가 지나가는 부분만 연산에 포함된다는 점과, 하나의 이미지에 같은 필터를 연달아 적용하기 때문에 가중치(그림에서는 w1, w2, w3, w4)가 공유되어 기본 인공 신경망보다 학습의 대상이 되는 변수가 적다는 점이 차이점이라고 할 수 있습니다. 이처럼 합성곱 연산도 입력과 가중치의 조합으로 이루어진 연산이기 때문에 비선형성을 추가하기 위해서는 활성화 함수가 필요합니다. 이때 4장에서 언급했던 렐루를 주로 사용하는데, 이쯤에서 렐루가 어떤 특징을 가지고 있는지 설명하고 넘어가겠습니다. 렐루 함수에는 여러 종류가 있는데 크게 다음과 같이 세 가지 정도로 나눌 수 있습니다.
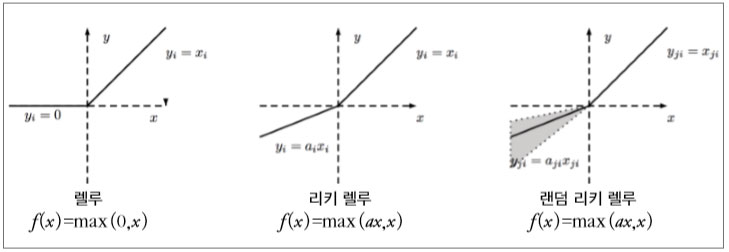
다양한 렐루 함수의 종류
먼저 기본 렐루 함수부터 살펴보죠. 기본 렐루 함수는 단순히 0 이하의 값이 들어오면 활성화 값을 0으로 맞추고 그 이상의 값이 들어오면 값을 그대로 전달합니다. 어떤 값이 들어오든 0에서 1의 값으로 맞춰주는 시그모이드 함수나 -1에서 1로 맞춰주던 하이퍼볼릭 탄젠트 함수와 달리 렐루는 입력으로 들어온 값, 즉 자극이 0 이상일 때 그대로 전달해주기 때문에, 전파되는 값들이 크고 역전파되는 값들 역시 yx = 를 미분하면 1이 나오기 때문에 기울기 값이 그대로 전파되므로 학습 속도가 빠릅니다. 또한 연산 과정에서 시그모이드나 하이퍼볼릭 탄젠트는 지수 연산이 들어가는데 비해 렐루는 값을 그대로 전달해주기 때문에 속도 면에서도 장점이 있습니다. 하지만 일반 렐루는 어느 순간 큰 손실이 발생하여 가중치와 편차가 마이너스로 떨어지는 경우, 어떠한 입력값이 들어와도 활성화 값이 0이 되는 다잉 뉴런dying neuron이라는 현상이 일어나기도 합니다. 예를 들어 업데이트된 가중치와 편차가 -5와 -3이고 입력값들은 정규화되어 -1에 서 1 사이의 값을 가진다면 어떠한 값이 들어와도 결괏값이 0보다 작기 때문에 해당 뉴런은 영원히 업데이트되지 않게 됩니다.
이런 문제를 해결하기 위해 나온 렐루의 변형된 형태로 리키 렐루leaky ReLU, 랜덤 리키 렐루randomized leaky ReLU 등이 있습니다. 리키 렐루는 수식을 f(x) = max(ax, x) 로 변형시키고 상수 a에 작은 값을 설정함으로써 0 이하의 자극이 들어왔을 때도 활성화 값이 전달되게 합니다. 예를 들어 a가 0.2라고 하면 0 이하의 자극에는 0.2를 곱해 전달하고 0보다 큰 자극은 그대로 전달하는 활성화 함수가 됩니 다. 이렇게 되면 역전파가 일어날 때, 0 이하인 부분에서는 가중치가 양의 방향 으로 업데이트되고 0보다 큰 부분에서는 음의 방향으로 업데이트되므로 다잉 뉴런 현상을 방지할 수 있습니다. 랜덤 리키 렐루의 경우는 a의 값을 랜덤하게 지정하는 활성화 함수입니다. 이번에는 이미지에 필터를 적용했을 때 실제로 어떤 결과가 나오는지 한번 보고 넘어가겠습니다. 다음 예시들은 합성곱 신경망처럼 스스로 학습된 필터들을 적용한 것이 아니라 사람이 직접 값을 지정한 필터들입니다. 먼저 이미지에서 경계선을 찾아주는 필터를 적용한 결과입니다

경계선 필터를 적용한 사례(http://setosa.io/ev/image-kernels/)
이렇게 경계선 필터를 사용하면 이미지에서 물체 간의 경계선을 쉽게 찾을 수 있습니다. 이는 원본 이미지에서 경계선에 대한 정보를 강조해서 보여주는 역할을 하고, 이를 통해 이미지의 특성을 분석하는 데 도움을 줍니다. 실제로 합성곱 신경망 모델을 학습시킨 후에 이미지를 학습된 필터에 통과시켜보면 사람이 직접 값을 지정했던 필터의 유사한 결과를 얻을 수 있습니다. 다음으로 같은 그림에 엠보스 필터를 적용한 결과 예시입니다.

엠보스 필터를 적용한 사례
엠보스 필터는 이미지에서 지정한 방향으로 깊이감을 강조해주는 역할을 합니다. 입력단과 첫 번째 은닉층 사이에는 이러한 역할을 하는 필터가 지정한 개수만큼 학습되고, 이를 통해 다양한 특징들을 뽑아내 다음 층으로 전달할 수 있습니다. 필터를 통해 뽑아낸 특성들이 중첩됨에 따라 모델은 더 복잡하고 다양한 형태를 구분할 수 있게 됩니다.
파이토치에 대해 자세히 알아보기 →
이전 글 : 최초의 버그와 최초의 컴파일러
다음 글 : 폰 노이만과 새로운 컴퓨터의 탄생
최신 콘텐츠